[김건우][AI 기초] 10. 선형회귀(Linear Regression) - 특성과 규제
작성자 : 김건우
(2024-05-15)
조회수 : 9187
[YOUTUBE] https://youtu.be/VttxVpComLU
[CODE] 영상 하단 설명란
#인공지능 #머신러닝 #선형회귀 #코딩
다항식과 다중특성을 이용한 선형회귀 구현 & 규제를 이용한 모델최적화
► 과소적합(under-fitting) vs 최적합(Optimal fitting) vs 과대적합(over-fitting)
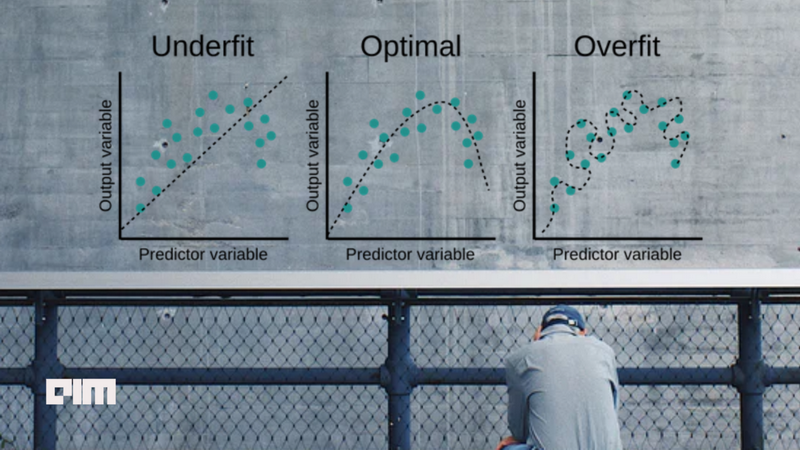
출처: Vijaysinh Lendave, Understanding Overfitting and Underfitting for Data Science, https://analyticsindiamag.com, June 8, 2021
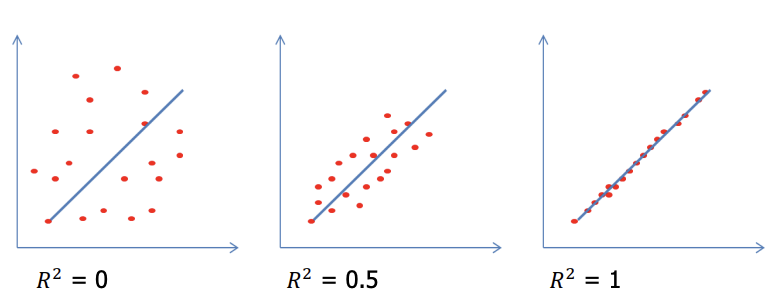
► 결정계수(R2)
. 회귀결과의 타당성을 객관적으로 평가하는 지표로 결정계수를 사용한다.
.결정계수이 값이 1에 가까우면 성능이 좋은 예측모델이라고 할 수 있다.
. SciKit-Learn에서 결정계수는 model.score() 함수로 구할 수 있다.
. 결정계수가 0에 가까울수록 성능이 좋지 않고, 1에 가까울수록 예측성능이 좋다고 할 수 있다.

► 선형회귀 vs Ridge(능선) 회귀 vs Lasso(올가미)
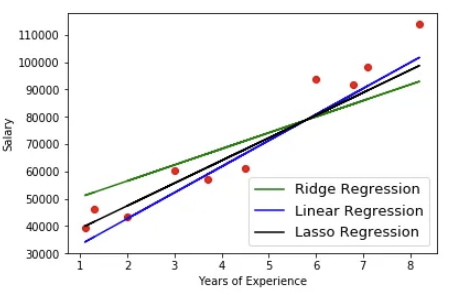
선형회귀: y = β0 + β1x1 + β2x2 + ··· βkxk
능성회귀(L2): y = β0 + β1x1 + β2x2 + ··· βkxk + λ(기울기) ²
올가미 회귀(L1): y = β0 + β1x1 + β2x2 + ··· βkxk + λ|기울기|
► 클래스(class) vs 인스턴스(instance)
lr = LinearRegression() # 클래스 = LinearRegression -> 인스턴스(변수) = lr
ridge = Ridge()
lasso = Lasso()