[참조]

Abaqus Tutorial - FEA of a Reinforced Concrete Column, 2019
https://www.youtube.com/watch?v=P7RH6apkhkQ
Abaqus FEA, Structural System Lab, 2022
https://www.dropbox.com/s/tsk1ibfd97ey0ws/Abaqus.pdf?dl=0
21 ABAQUS Tutorial: Defining Concrete Damage Plasticity Model + Failure and Element Deletion,, 2022
https://www.youtube.com/watch?v=wy84XGamn3g

 
(1) Part
(2) Property
(3) Assembly
(4) Step
(5) Interaction 
(6) Load
(7) Mesh
(8) Job
(9) Visualization

--------
[문제]
다음 기둥의 하중-변위 곡선을 그려라.

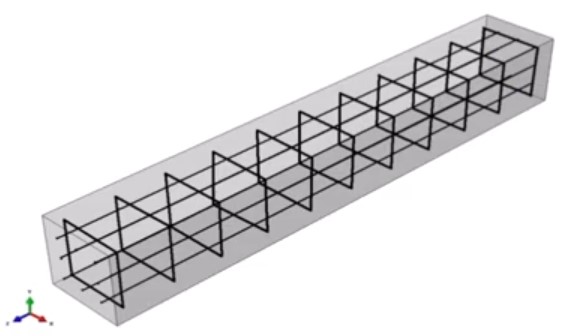
.단위: mm, kg, N

.모델 
-치수: 2000 x 300 x 300 mm
-경계조건: 하단 고정, 상단 자유
-수직하중: 270 kN 압축 (= 270,000/(300x300) = 3 N/mm2)
-수평하중: 200 mm 변위

.주근
-단면적: 254.47 mm2
-위치(x,y,z)
   62.5,   62.5,  2000.
   62.5,   150.,  2000.
   62.5,  237.5,  2000.
   150.,  237.5,  2000.
  237.5,  237.5,  2000.
  237.5,   150.,  2000.
  237.5,   62.5,  2000.
   150.,   62.5,  2000.

.스터럽
-단면적: 78.54 mm2 (240 x 240 mm)
-위치(x,y,z)
   30,  30,  1950

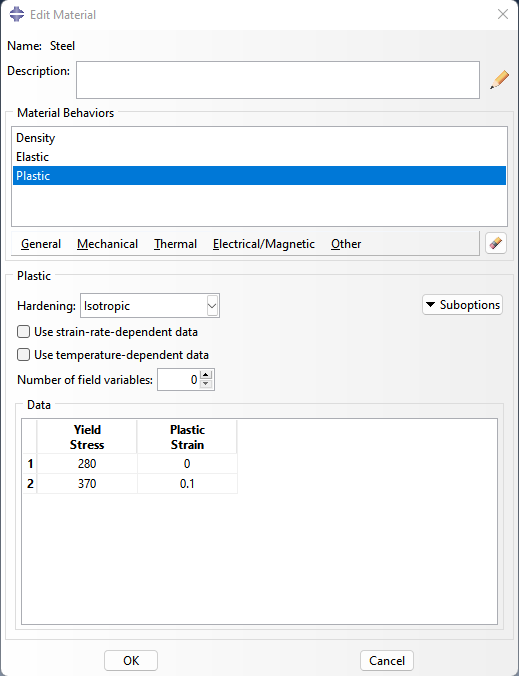
.재료: 강재
-rho = 7.8e-6 kg/mm3
-E = 200e3 (MPa), nu = 0.3
-Plastic(sigma-strain)
280 0
370 0.1

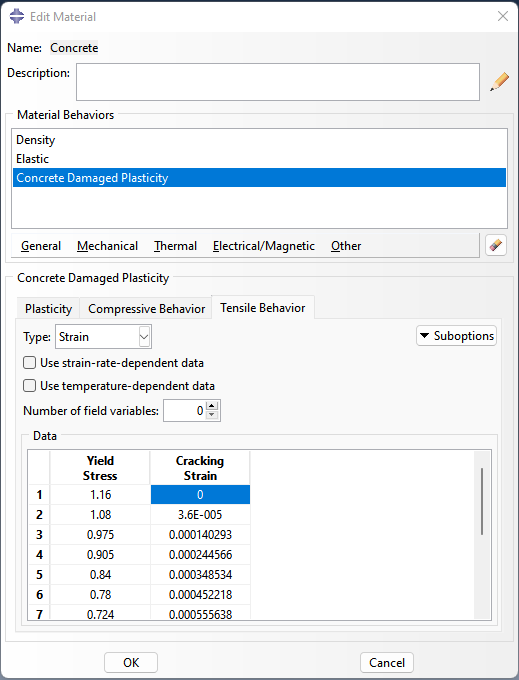
.재료: 콘크리트
-rho = 2.4e-6 kg/mm3
-E = 17585 (MPa), nu = 0.3
-Plasticity
Dilatation Angle: 30.5
Eccentricity: 0.1
fb0/fc0: 1.16
K: 0.666
Viscosity Parameter: 0.001

-Concrete Damage Plasticity
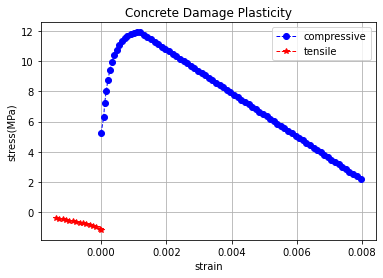
Compressive Behavior(sigma-strain)
5.23363173      0.000000000
6.27766432      0.000080031
7.21148249      0.000117560
8.03781640      0.000162279
8.76131374      0.000213877
9.38798871      0.000271954
9.92473606      0.000336046
10.37892424     0.000405661
10.75807052     0.000480297
11.06959380     0.000559456
11.32063606     0.000642662
11.51794157     0.000729462
11.66778274     0.000819438
11.77592203     0.000912203
11.84760087     0.001007408
11.88754784     0.001104736
11.90000000     0.001203903
11.74130500     0.001314519
11.58261000     0.001425136
11.42391500     0.001535752
11.26522000     0.001646369
11.10652500     0.001756985
10.94783000     0.001867602
10.78913500     0.001978218
10.63044000     0.002088835
10.47174500     0.002199451
10.31305000     0.002310068
10.15435500     0.002420684
9.99566000      0.002531301
9.83696500      0.002641918
9.67827000      0.002752534
9.51957500      0.002863151
9.36088000      0.002973767
9.20218500      0.003084384
9.04349000      0.003195000
8.88479500      0.003305617
8.72610000      0.003416233
8.56740500      0.003526850
8.40871000      0.003637466
8.25001500      0.003748083
8.09132000      0.003858699
7.93262500      0.003969316
7.77393000      0.004079932
7.61523500      0.004190549
7.45654000      0.004301165
7.29784500      0.004411782
7.13915000      0.004522398
6.98045500      0.004633015
6.82176000      0.004743632
6.66306500      0.004854248
6.50437000      0.004964865
6.34567500      0.005075481
6.18698000      0.005186098
6.02828500      0.005296714
5.86959000      0.005407331
5.71089500      0.005517947
5.55220000      0.005628564
5.39350500      0.005739180
5.23481000      0.005849797
5.07611500      0.005960413
4.91742000      0.006071030
4.75872500      0.006181646
4.60003000      0.006292263
4.44133500      0.006402879
4.28264000      0.006513496
4.12394500      0.006624112
3.96525000      0.006734729
3.80655500      0.006845346
3.64786000      0.006955962
3.48916500      0.007066579
3.33047000      0.007177195
3.17177500      0.007287812
3.01308000      0.007398428
2.85438500      0.007509045
2.69569000      0.007619661
2.53699500      0.007730278
2.37830000      0.007840894
2.21960500      0.007951511

Tensile Behavior(sigma-strain)
1.160     0.000000000
1.080     0.000036000
0.975     0.000140293
0.905     0.000244566
0.840     0.000348534
0.780     0.000452218
0.724     0.000555638
0.672     0.000658814
0.624     0.000761762
0.580     0.000864499
0.538     0.000967040
0.500     0.001069399
0.464     0.001171590
0.431     0.001273623
0.400     0.001375511

(1) Part
3개의 Part를 사용한다.
.Concrete: 2000 x 300 x 300 mm
.Bar: 2000 mm
.Stirrup: 240 x 240 mm

  

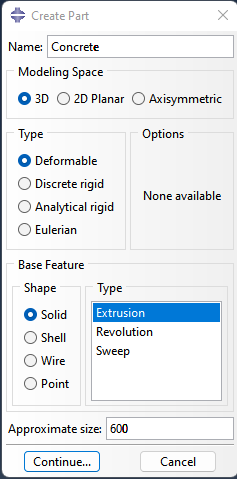
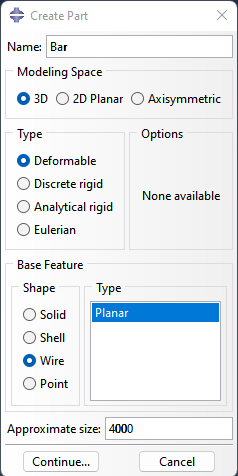
(2) Property
2개의 재료 성질을 생성한다.
.강재
.콘크리트

 

 

  

 

 

3개의 단면 성질을 생성한다.
.Section-Concrete
.Section-Bar
.Section-Stirrup

 

 

  

 

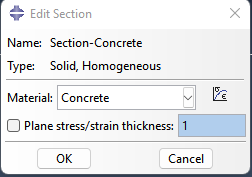
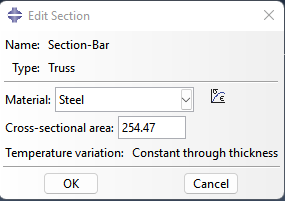
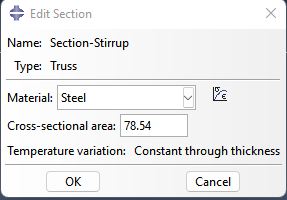
Part들에 해당 Section들을 Assign한다.
.Uncheck 'create set'

 

 

 

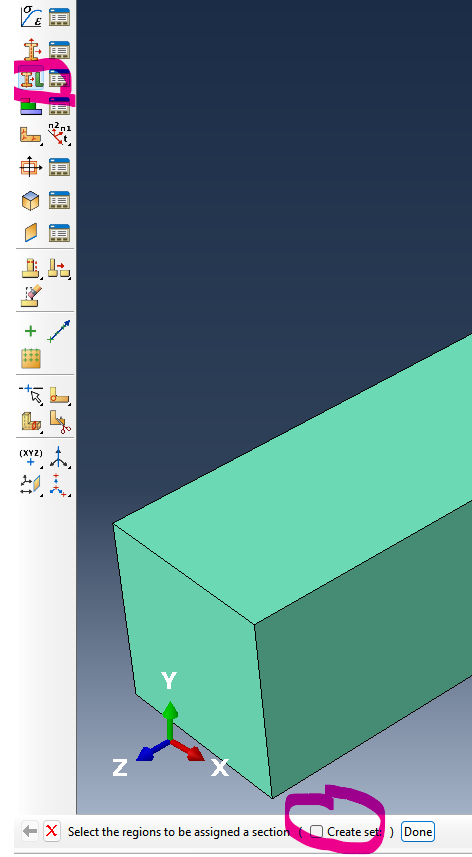
(3) Assembly
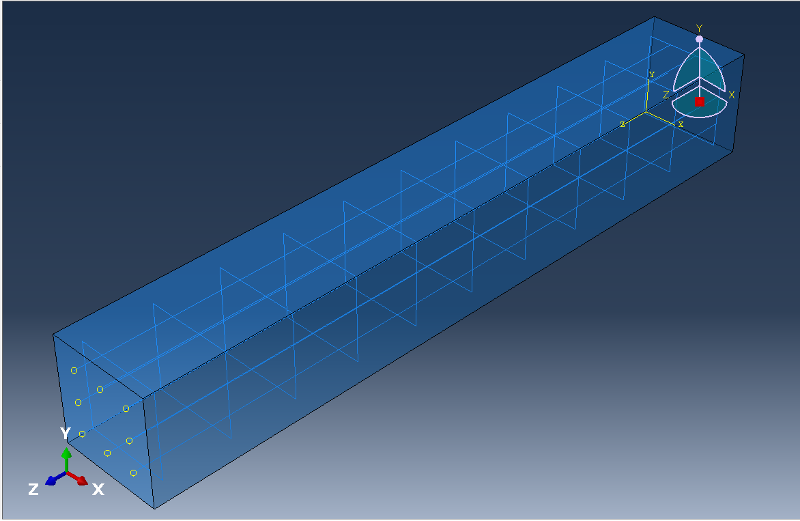
Concrete, Bar, Stirrup 순으로 Instance를 만든다.
Bar의 경우 Instance를 생성한 후, 설정된 Datum과 회전과 이동을 통해 옳은 위치로 옮긴다.
Stirrup의 경우 Instance를 생성한 후, 설정된 Linear Pattern과 회전과 이동을 통해 옳은 위치로 옮긴다.

 

 

  

 

(4) Step
2가지 Step이 필요하다.
.하중
.변위

.Create Step: General | Static, General

 

 

 

(5) Interaction
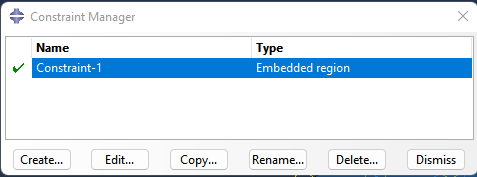
Concrete에 Bar와 Stirrup이 Embedded로 host한다. 

 

 

 

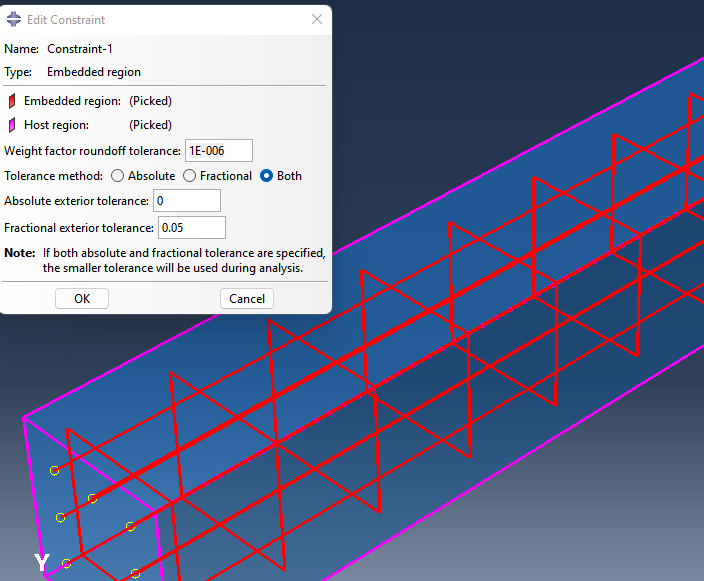
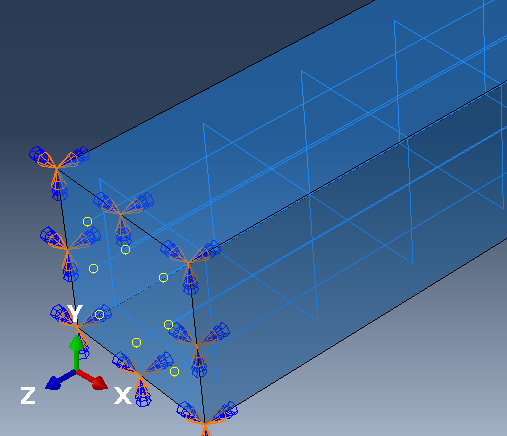
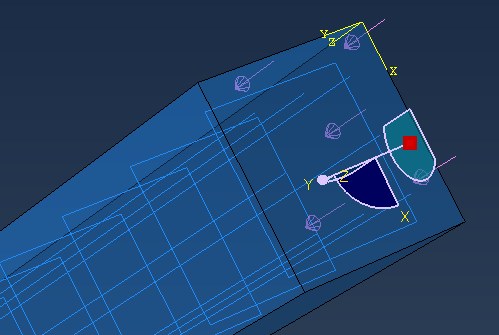
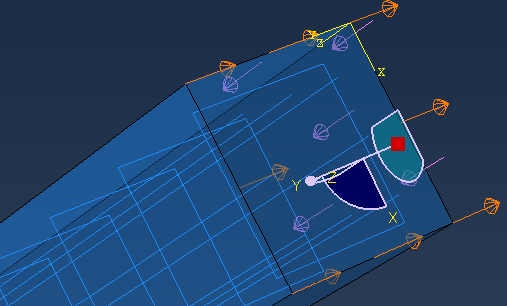
(6) Load
.Step: Initial
Create Boundary Condition: 1단 고정
.Step: Step-1
Create Load: 3 N/mm2
.Step: Step-2
Create Boundary Condition: -200 mm

  

(7) Mesh
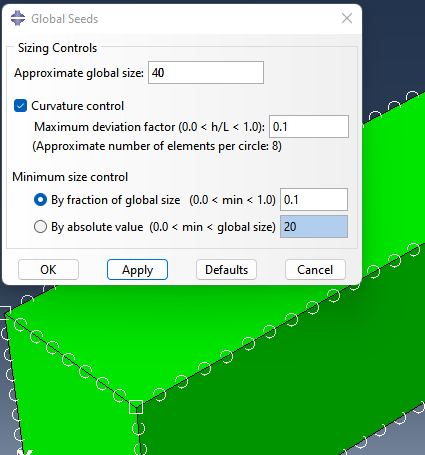
3개 Part에 대해 Seed와 Mesh 순서로 수행한다.
.Concrete: Seed size = 40
.Bar: Mesh > Element Type : Truss
.Stirrup: Mesh > Element Type : Truss

(8) Job
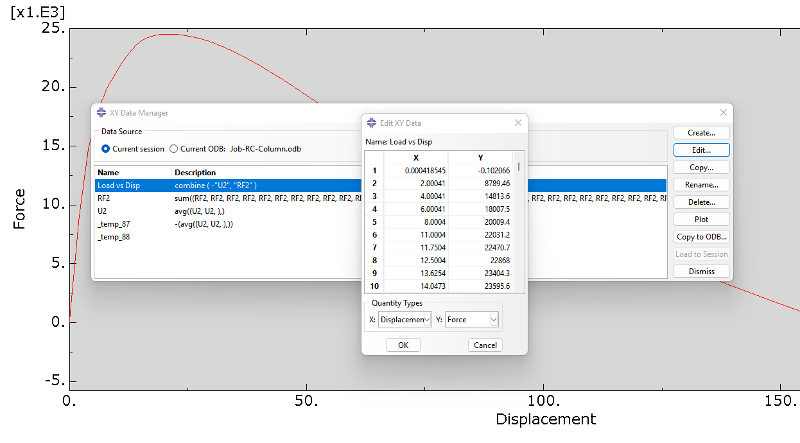
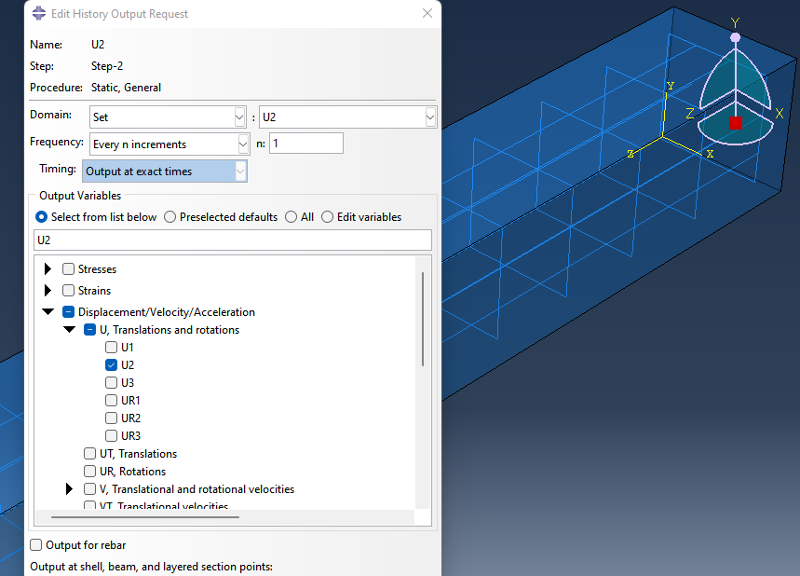
그림을 그리기 위해 Step 모듈로 들어가서, Tool > Set(RF, )를 정의하고, Create History를 정의한다.

 

(9) Visualization
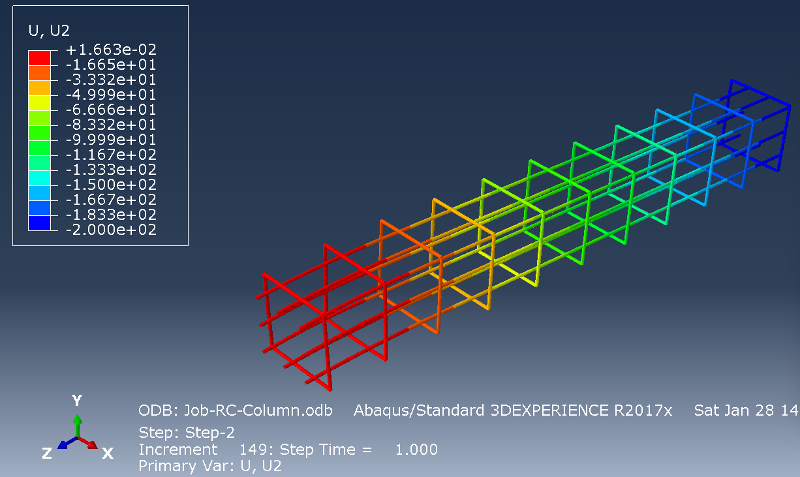
.Field Output Dialog: Primary | RF | RF2

  

.Create Display Group: 
.Field Output Dialog: Primary | U | U2

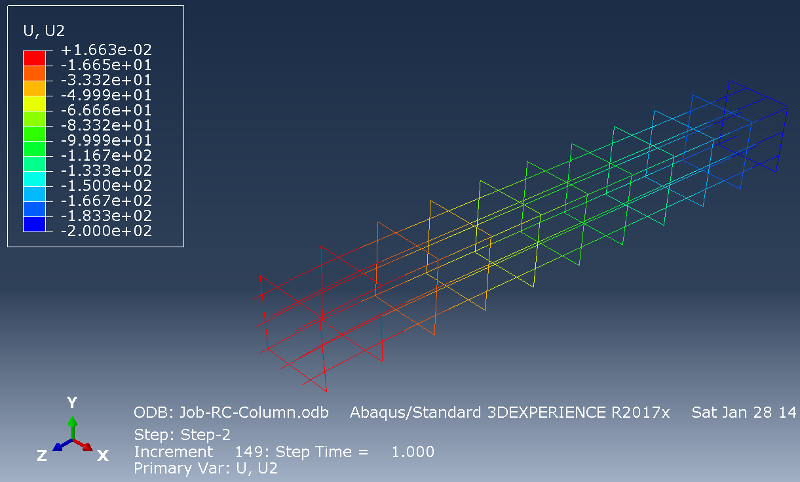
.View > ODB Display Options...: (Check) Render beam profiles 
 

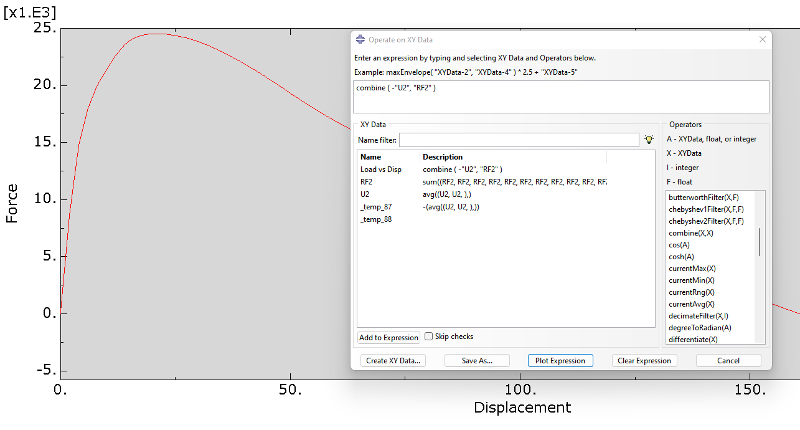
.Create XY Data: ODB history output
.Create XY Data: U2 vs RF2
.Create XY Data: RF2~sum(두 지점 반력의 합)
.Create XY Data: U2~avg(두 지점 변위 평균)
.Create XY Data: Displacement vs Force ~combine(U2, RF2)

.XY Data Manager