출처: 길벗
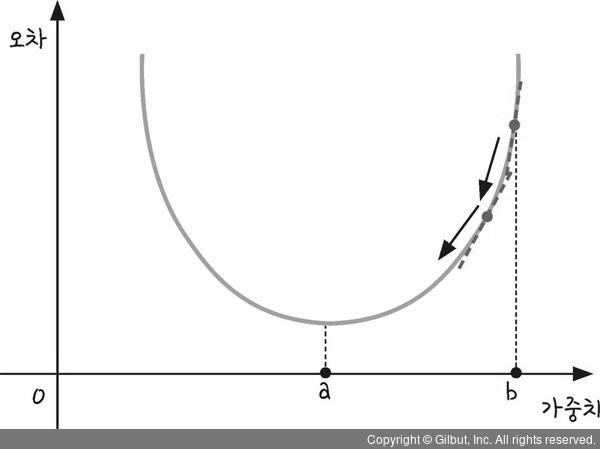
경사 하강법(Gradient Descent)은 최적화 기법 중 하나로, 함수의 기울기를 따라 내려가면서 최적의 값을 찾는 알고리즘이다. 머신러닝과 딥러닝에서 비용 함수(Cost Function)를 최소화하는 데 사용된다.
경사 하강법은 특정 함수의 기울기를 이용해 "최소값(Local Minimum)"을 찾아가는 반복적인 최적화 방법이다.
경사 하강법은 다음과 같은 수식으로 표현된다:
\[ \theta_{t+1} = \theta_t - \alpha \nabla J(\theta_t) \]
\( \theta_t \): 현재 가중치
\( \alpha \): 학습률 (Learning Rate)
\( \nabla J(\theta_t) \): 비용 함수의 기울기
이 수식을 반복적으로 적용하여 최적의 \( \theta \) 값을 찾는다.
경사 하강법에서 경삿값(기울기)은 손실 함수(비용 함수)를 미분하여 구한다. 예를 들어 손실 함수가 다음과 같이 주어졌다고 하자.
\[ y = (x-3)^2 + 15 \]
이 손실 함수를 \(x\)에 대해 미분하면 경삿값(기울기) \(y'\)을 구할 수 있다.
\[ y' = 2(x-3) \]
여기에 \( x=7 \)을 대입하면 다음과 같이 경삿값을 계산할 수 있다.
\[ y' = 2 \times (7-3) = 2 \times 4 = 8 \]
따라서 \( x=7 \)에서의 경삿값은 8이며, 경사 하강법은 이 경삿값(기울기)에 학습률 \(\alpha\)를 곱한 만큼 \(x\)를 반대 방향(기울기가 작아지는 방향)으로 이동시키면서 최솟값을 찾아간다.
[예시]
\[ \begin{align} \omega_{ij}^{new} &= \omega_{ij}^{old} + \Delta\omega_{ij} \\ &= \omega_{ij}^{old} + L \cdot \frac{\partial \omega_{ij}}{\partial L} \\ b_{ij}^{new} &= b_{ij}^{old} + \Delta b_{ij} \\ &= b_{ij}^{old} + L \cdot \frac{\partial b_{ij}}{\partial L} \end{align} \]