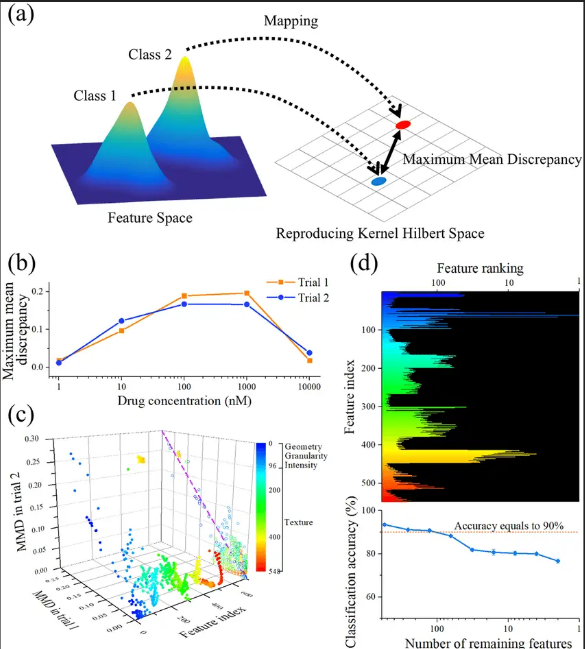
🔗 관련 문서: Wikipedia - Maximum Mean Discrepancy

MMD (Maximum Mean Discrepancy) - 최대 평균 불일치

MMD는 두 확률 분포(P, Q) 간의 차이를 측정하는 커널 기반 통계량이다. 생성 모델의 평가, 도메인 적응, 통계적 검정 등에 활용된다.

1. 개요

Maximum Mean Discrepancy (MMD)는 두 분포가 동일한지를 평가하기 위해 샘플 평균 임베딩을 비교하는 기법이다.

2. MMD의 정의

2.1 핵심 아이디어

MMD는 두 분포 \( P \)와 \( Q \)의 평균 임베딩 차이로 정의된다:

\[ \text{MMD}^2(P, Q) = \left\| \mathbb{E}_{x \sim P}[\phi(x)] - \mathbb{E}_{y \sim Q}[\phi(y)] \right\|^2 \]

2.2 실제 계산 방식

샘플 집합 \( X, Y \)에서 MMD를 커널 함수로 근사:

\[ \text{MMD}^2(X, Y) = \frac{1}{m^2} \sum_{i,j} k(x_i, x_j) + \frac{1}{n^2} \sum_{i,j} k(y_i, y_j) - \frac{2}{mn} \sum_{i,j} k(x_i, y_j) \]

일반적으로 사용되는 커널: \[ k(x, y) = \exp\left(-\frac{\|x - y\|^2}{2\sigma^2}\right) \]

2.3 요약

3. 활용

• 도메인 적응: 입력 도메인 간 분포 차이를 줄여 일반화 향상
• 생성 모델 평가: GAN이 만든 분포와 실제 데이터 비교
• 통계적 검정: 분포 동일성 여부 확인

4. 파이썬 코드

import numpy as np
from scipy.spatial.distance import cdist

def gaussian_kernel(x, y, sigma=1.0):
    return np.exp(-cdist(x, y, 'sqeuclidean') / (2 * sigma ** 2))

def compute_mmd(X, Y, sigma=1.0):
    K_xx = gaussian_kernel(X, X, sigma)
    K_yy = gaussian_kernel(Y, Y, sigma)
    K_xy = gaussian_kernel(X, Y, sigma)
    return np.mean(K_xx) - 2 * np.mean(K_xy) + np.mean(K_yy)
  

5. 장점과 단점

6. 결론

MMD는 분포 간 차이를 정량적으로 측정할 수 있는 강력한 도구로, 생성 모델 평가, 도메인 적응, 통계 검정 등에서 널리 활용된다.