🔗 관련 문서: Wikipedia - Support Vector Machine

SVM (Support Vector Machine)

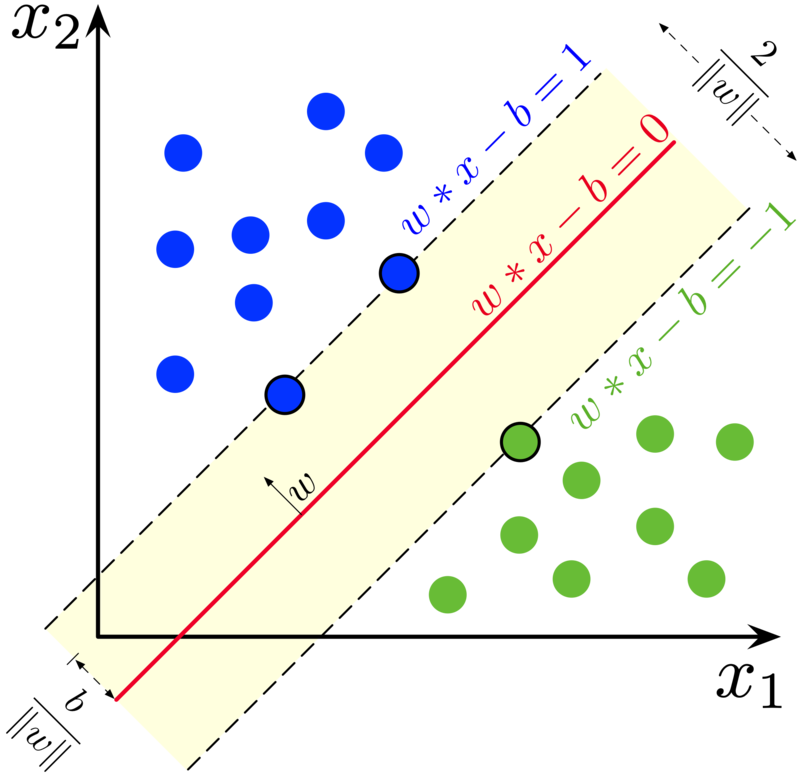
SVM은 지도 학습(Supervised Learning) 방식의 분류(Classification) 및 회귀(Regression) 알고리즘으로, 주어진 데이터를 가장 잘 구분하는 초평면(hyperplane)을 찾아내는 것을 목표로 한다.

두 클래스 사이의 마진(margin)을 최대화함으로써 일반화 성능을 높이는 것이 SVM의 핵심 원리이다.

(1) 정의와 핵심 개념

Support Vector Machine은 데이터를 구분하는 선형 또는 비선형의 결정 경계를 설정하며, 가장 가까운 샘플들(Support Vectors)로부터 최적의 분리 초평면을 계산한다.

마진이 넓을수록 새로운 데이터에 대해 더 나은 일반화 성능을 기대할 수 있다. 선형으로 구분되지 않는 경우에는 커널 함수(Kernel Function)를 통해 고차원 공간으로 데이터를 사상시켜 분리가 가능하도록 한다.

(2) 알고리즘 원리

1. 초평면을 정의할 수 있도록 데이터를 수학적으로 표현한다.
2. 각 클래스에서 가장 경계에 가까운 데이터를 서포트 벡터로 선정한다.
3. 이 서포트 벡터들 사이의 거리를 마진이라 하며, 이 마진을 최대화하는 초평면을 찾는다.
4. 비선형 분류 문제의 경우 커널 트릭을 이용해 고차원으로 변환한다.

(3) 장점과 한계

장점

• 고차원 데이터에도 효과적으로 작동한다.
• 작은 데이터셋에서도 높은 성능을 낼 수 있다.
• 마진 최적화를 통해 과적합(overfitting)을 방지한다.

한계

• 대용량 데이터에 적용할 경우 계산 비용이 높다.
• 하이퍼파라미터 설정과 커널 선택에 민감하다.

(4) 개념도

다음은 SVM의 결정 경계와 서포트 벡터를 시각적으로 나타낸 예시이다.

한반도의 DMZ는 38선에서 ±5 km이다.

• 결정 경계(Decision Boundary): 분류를 위한 기준선
• 서포트 벡터(Support Vector): 결정 경계와 가장 가까운 위치에 있는 데이터
• 마진(Margin): 결정 경계와 서포트 벡터 사이의 거리