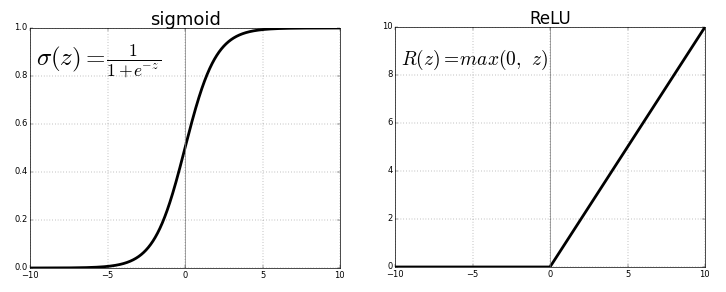
Sigmoid(시그모이드) 함수는 딥러닝에서 널리 사용되는 활성화 함수 중 하나로, 입력 값을 0과 1 사이의 값으로 변환한다. 함수의 그래프가 S자 형태를 띠기 때문에 이런 이름이 붙었다.
Sigmoid 함수는 입력 값을 0과 1 사이의 값으로 압축하는 비선형 활성화 함수다. 주로 신경망에서 이진 분류 문제에 사용되며, 출력값을 확률로 해석할 수 있다.
Sigmoid 함수는 다음과 같이 정의된다.
\[ \sigma(z) = \frac{1}{1 + e^{-z}} \]입력 값이 클수록 1에 가까운 값이 출력되며, 입력 값이 작을수록 0에 가까운 값이 출력된다.
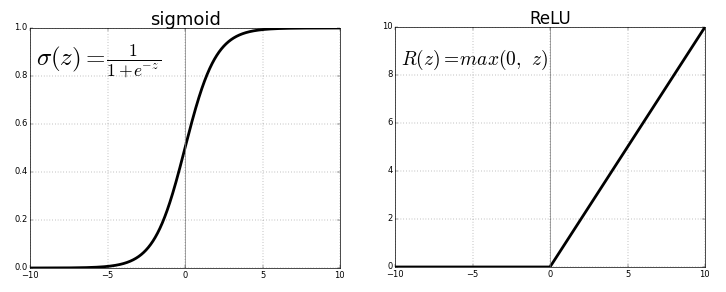
Sigmoid 함수의 미분은 다음과 같이 표현된다.
\[ \sigma'(z) = \sigma(z) \cdot [1 - \sigma(z)] \]
즉, 입력값 \( z \)에 대한 Sigmoid 함수의 도함수는 Sigmoid 출력값을 기반으로 계산된다. 이 특성은 역전파 과정에서 효율적인 계산을 가능하게 한다.
예제
예를 들어, 입력값 \( z = 0 \)일 때:
\[ \sigma(0) = \frac{1}{1 + e^{0}} = \frac{1}{2} = 0.5 \] \[ \sigma'(0) = 0.5 \cdot (1 - 0.5) = 0.25 \]따라서 입력값이 0일 때 Sigmoid 함수의 출력은 0.5이고, 그 미분값은 0.25이다.