Neural Network(NN; Artificial NN; ANN) 신경망(인공신경망)

신경망(Neural Network)은 인간의 뇌에서 영감을 받아 개발된 머신러닝 모델로, 뉴런(Neuron)과 그 연결 구조를 모방하여 데이터를 처리한다.

1. 신경망의 구조

신경망은 "입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)"으로 구성된다. 각 층의 뉴런들은 가중치(Weight)와 활성화 함수(Activation Function)를 사용하여 정보를 전달하고 변환한다.

2. 정보처리 과정

1) 입력 신호 수집

2) 신호 합산

3) 활성화 함수 적용

4) 출력 전달

인공신경망 방식으로 만든 인공지능에서는 입력한 데이터가 여러 레이어를 지나가면서 특정한 신호로 전달된다. 그러면 최종적으로 신호가 남자 쪽으로 가는지, 여자 쪽으로 가는지를 판단하여, 둘 중 어느 쪽으로 신호가 많이 가는지를 살펴본 후 신호가 많이 간 쪽 성별이라고 판단을 내린다.

1) 입력 신호 수집

뉴런의 가지돌기가 신호를 입력받음

2) 신호 합산

입력된 신호를 가중치를 적용하여 합산
가중합(Weighted Sum)이란 입력값과 가중치를 곱한 뒤 편향(Bias)을 더한 값을 말한다.

3) 활성화 함수 적용

특정 임계값(역치; threshold; action potential)을 넘으면 신호가 전달됨

활성화 함수(Activation Function)는 인공신경망에서 각 뉴런이 입력을 받아 출력을 계산하는 함수이다. 활성화 함수를 사용하는 이유는 두 가지이다.

• 첫째, 출력값을 0~1 사이의 값으로 반환해야 하는 경우에 사용한다. 이진 분류 문제 등이 여기에 해당한다.
• 둘째, 비선형을 위해 사용한다. 만약 가중치(w)와 편향(b)을 구하는 과정이 모두 선형의 수식들만 겹친다면 무슨 일이 일어날까? 어떤 복잡한 과정을 거쳐도 \( y = wx + b \) 라는 단순한 형식을 벗어날 수 없어 선형 구조만 유지된다. 예를 들어, 선형함수인 \( f(x) = wx \)식이 있다고 가정해 보자. 이때 은닉층을 2개 사용한다면, 식은 \[ f(f(f(x))) = (w (w (w x))) = kx \] 로 단순하게 변형된다. 은닉층을 20개 사용한다고 해도 동일한 결과가 나온다. 즉, 선형함수로는 은닉층을 여러 개 추가해도 은닉층을 1개 추가한 것과 차이가 없기 때문에 정확한 결과를 위해서는 비선형 함수, 즉 활성화 함수가 필요하다.

활성화 함수의 유형 [링크]

• 시그모이드(Sigmoid) 함수 또는 로지스틱(Logistic) 함수
• 하이퍼볼릭 탄젠트(Hyperbolic Tangent) 함수
• 렐루(ReLU) 함수
• 소프트맥스(SoftMax) 함수
• 리키렐루(LeakyReLU) 함수

4) 출력 전달

• 순전파(Forward Propagation)
• 손실함수(Loss Function)
• 옵티마이저(Optimizer)
• 역전파(Backpropagation)

활성화된 신호가 다음 층으로 전달됨

딥러닝은 순전파, 손실함수, 옵티마이저, 역전파 과정을 거치면서 학습한다.

▶ 순전파(Forward Propagation) [링크]

네트워크(신경망)를 구성하기 위해서는 먼저 은닉층의 수와 각 은닉층의 뉴런 수, 활성화 함수, 손실함수 등과 같은 하이퍼파라미터를 결정해야 한다. 네트워크가 구성된 이후에는 입력값이 은닉층을 지나면서 곱해진 가중치값의 결과가 출력층으로 향한다. 출력층에서는 모든 연산을 마친 예측값이 출력된다. 즉, 입력층에서 출력층 방향으로 연산이 진행되면서 최종 출력값(예측값)이 도출되는 과정을 순전파라고 한다.

▶ 손실함수(Loss Function) [링크]

손실함수는 예측값과 실제값의 차이를 구하는 함수이다. 이 두 값의 차이가 클수록 손실함수의 값은 커지고, 차이가 작을수록 손실함수의 값도 작아진다. 회귀에서는 평균제곱오차(MSE, Mean Squared Error), 분류 문제에서는 크로스 엔트로피(Cross Entropy)를 손실함수로 많이 사용한다. 손실함수가 중요한 이유는 딥러닝의 학습 과정에서 손실함수의 값이 최소가 되는 두 개의 매개변수인 가중치(w)와 편향(b)을 찾을 수 있기 때문이다.

▶ 옵티마이저(Optimizer) [링크]

손실함수의 값을 줄여나가면서 학습하는 딥러닝은 어떤 옵티마이저를 사용하느냐에 따라 성능이 달라진다. 옵티마이저란 딥러닝에서 학습 속도를 빠르고 안정적이게 만드는 것을 뜻한다. 배치라는 개념을 함께 이해하면 좋은데, 배치(Batch)란 가중치 등 매개변수의 값을 조정하기 위해 사용하는 데이터의 양을 뜻한다. 전체 데이터(전체 배치)를 가지고 매개변수(가중치, 편향)의 값을 조정할 수 있고, 정해진 양의 데이터(미니 배치)만 가지고 매개변수의 값을 조정할 수도 있다. 일반적으로 전체 배치(Full Batch, 전체 데이터)를 한 번에 학습하게 되면 계산량이 많아질 뿐만 아니라 속도도 느려질 수 있기 때문에 미니 배치(Mini Batch)를 이용한 학습을 한다.

▶ 역전파(Backpropagation) [링크]

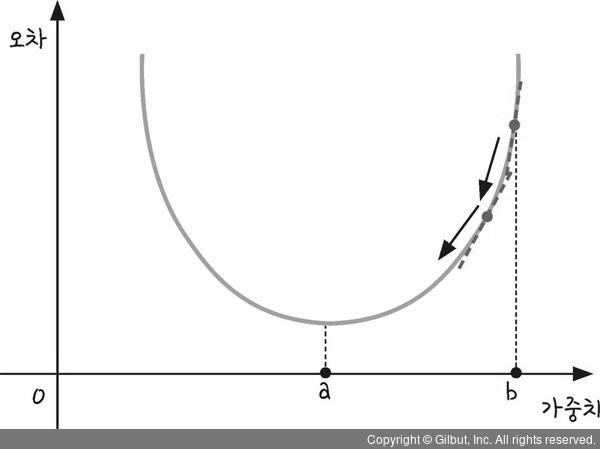
층이 하나만 있으면, 한 번의 경사하강법으로 뉴런과 뉴런을 연결한 가중치를 수정할 수 있다. 그러나 여러 개의 층이 있다면 문제가 복잡하다. 이렇게 많은 가중치를 어떻게 바꿀 수 있을까? 뒤에 있는 층의 가중치에서부터 앞에 있는 층의 가중치로 수정해 나가는 방법이 역전파 알고리즘이다.

역전파(Backpropagation; Chain Rule)란 오차(예측값과 실제값의 차이)를 역방향으로 전파시키면서 (출력층 → 은닉층 → 입력층) 가중치를 업데이트하는 것이다.

역전파는 경사 하강법을 이용해 오차를 줄이는 방향으로 가중치를 수정한다. 가중치를 수정할 때에는 순전파에서 계산한 결과 \( y = f(x) \)의 편미분값을 오차에 곱해 출력층 → 은닉층 → 입력층 순서로 전달한다. 이때 편미분을 사용하는 이유는 많은 노드들에 부여되는 모든 가중치값을 전부 고려하지 않고 계산하려는 노드와 연결된 가중치값만을 고려할 수 있기 때문이다.

3. 신경망의 발전 과정

인공신경망은 인간의 뇌 신경망(Neural Network) 구조를 모방하여 정보를 처리하고 학습하는 알고리즘이다. 그 발전 과정은 수십 년에 걸쳐 점진적으로 이루어졌으며, 여러 시대적 전환점을 거치며 현재의 딥러닝 기술로 이어졌다.

• 1943년: 매컬러(McCulloch)와 피츠(Pitts)가 최초의 뉴런 모델 제안
• 1950~60년대: 프랭크 로젠블랫(Frank Rosenblatt)의 퍼셉트론 개발
• 1980년대: 다층 퍼셉트론(MLP)과 역전파(Backpropagation) 알고리즘 등장
• 2000년대 후반: GPU 발전과 함께 딥러닝의 급격한 성장
• 2012년: AlexNet이 이미지넷 대회에서 혁신적인 성과 달성

1) 퍼셉트론의 등장

1958년, 프랭크 로젠블렛(Frank Rosenblatt)은 최초의 인공신경망 모델인 퍼셉트론(Perceptron)을 제안하였다.

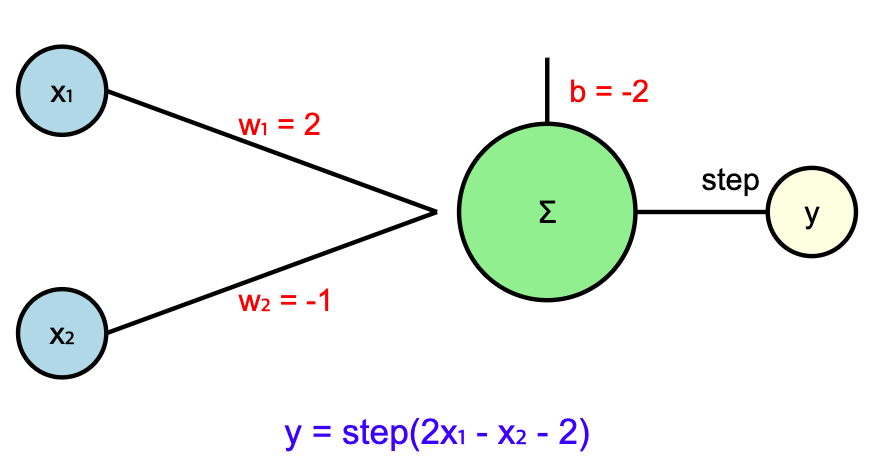
퍼셉트론이란 신호(x₁, x₂)를 입력값으로 받아 가중치(w₁, w₂)를 곱하고, 그 결과를 합산한 뒤 활성화 함수를 통해 출력값(y)을 결정하는 알고리즘이다.

퍼셉트론은 간단한 선형 분류 문제를 해결할 수 있었으나, XOR 문제와 같이 선형적으로 분리되지 않는 데이터는 처리할 수 없다는 한계가 존재했다.

2) 역전파 이전의 한계

1969년, 마빈 민스키(Marvin Minsky)와 세이무어 파퍼트(Seymour Papert)는 저서 『퍼셉트론』에서 퍼셉트론의 한계를 지적하며, 다층 구조가 필요함을 주장하였다. 즉, 당시의 퍼셉트론으로는 XOR 연산이 절대 불가능하며, 다층 퍼셉트론을 통해 XOR 연산에 대한 문제는 해결될 수 있지만, 각각의 가중치(Weight)와 편항(Bias)을 학습시킬 효과적인 알고리즘이 부재하였다.

이러한 배경 속에서 인공신경망에 대한 관심은 줄어들게 되었으며, 이 시기는 종종 "AI 겨울(AI Winter)"이라 불린다.

5년 후인 1974년, 폴 워보스가 박사과정 논문에서 다층 구조의 가중치와 편항을 학습시키기 위한 역전파(Backpropagation)를 제안하였다. 기존의 전방향(Feedforward) 학습을 통해 가중치와 편향을 수정하는 것이 아니라,
전방향에 대한 학습 결과를 보고, 뒤로 가면서 가중치와 편향을 수정하는 알고리즘이다.
즉, 신경망의 오차(예측값 - 실제값)를 출력층에서부터 입력층으로 피드백하여 각층(Layer)의 가중치와 편향을 업데이트 하는 알고리즘이다.

1986년, 데이비드 럼멜하트(David Rumelhart)와 제프리 힌튼(Geoffrey Hinton) 등의 연구자들에 의해 또 다른 역전파(Backpropagation) 알고리즘이 제안되면서 다층 신경망의 학습이 가능해졌다. 이는 인공신경망의 연구에 다시 활력을 불어넣었다.

이후 인공신경망 연구는 큰 진전이 있었지만, 다음과 같은 이유로 긴 침체기에서 벗어나지 못했다.

1. 신경망의 깊이가 깊어질수록 (학습력이 좋아져야 하는데) 원하는 결과는 얻을 수 없다. 즉, 역전파를 수행할 때 출력층에서 멀리 떨어진 층에서는 기울기가 급속히 작아지는 기울기 소멸(Vanishing Gradient) 문제와 기울기가 너무 커지는 기울기 발상(Exploding Gradient) 문제가 발생해 학습력이 떨어졌다.
2. 신경망 학습에 최적화된 하이퍼파라미터에 대한 이론적인 근거가 없다.

3) 딥러닝의 출현

깊었던 침체기에도 불구하고 인공신경망에 대한 연구는 꾸준히 진행되었다. 2006년, 역전파를 고안하였던 제프리 힌턴 교수는 "A fast learning algorithm for deep belief nets"라는 논문을 통해 가중치의 초기값을 제대로 설정하면 깊이가 깊은 신경망도 학습이 가능하다는 연구를 선보였다. 즉, 신경망을 학습시키기 전에 계층(예: 입력층, 은닉층) 단위의 학습을 거쳐 더 나은 초기값을 얻는 방식의 사전훈련(Pre-training) 방식을 제안한 것입니다.

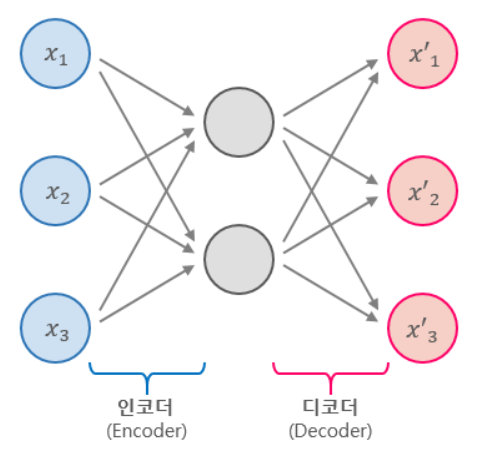
이어서 2007년에는 벤지오(Bengio) 팀이 "Greedy layer-wise training of deep networks"라는 논문을 통해 오토인코더(Autoencoder)를 사용한 좀 더 간단한 사전훈련 방법을 제안했다. 이러한 모든 노력을 통해 비로소 깊은 신경망에서도 학습이 가능하게 되었다.

그리고 이때부터 인공신경망(Neural)이라는 용어 대신 "딥(Deep)"이라는 용어를 사용하기 시작했다. 길고 긴 침체기 동안 인공신경망이라는 용어만 들어가도 논문 채택이 거절당할 정도로 부정적 인식이 강했기 때문에 사람들의 이목을 끌 수 있는 새로운 단어가 필요했기 때문이다. 그래서 2006년부터는 딥러닝(Deep Learning)이라는 용어가 사용되기 시작했다.

[Note] 사전훈련(Pre-training)이란?
선행학습이라고도 부르며, 다층 퍼셉트론에서 가중치와 편향을 제대로 초기화시키는 방법이다.

이후 컴퓨팅 파워의 향상, 대규모 데이터의 등장, GPU의 활용 등과 맞물려 2010년대에는 딥러닝(Deep Learning)이 급속도로 발전하였다. 딥러닝은 이미지 인식, 음성 인식, 자연어 처리 등 다양한 분야에서 획기적인 성과를 이루었다.

4. 신경망의 종류

• 퍼셉트론(Perceptron): 가장 기본적인 신경망 모델
• 다층 퍼셉트론(MLP): 은닉층이 추가된 구조, 비선형 문제 해결 가능
• 컨볼루션 신경망(CNN): 이미지 처리에 최적화된 신경망
• 순환 신경망(RNN): 시퀀스 데이터(음성, 번역)에 적합
• 트랜스포머(Transformer): 최신 자연어 처리(NLP) 모델의 기반